Sieve of Eratosthenes - Program to find all prime numbers smaller than a given number

Sieve of Eratosthenes is a very old algorithm to find all the prime numbers up to a given limit. For example, we can find all the prime numbers up to, say 101, using this algorithm in a very efficient manner.

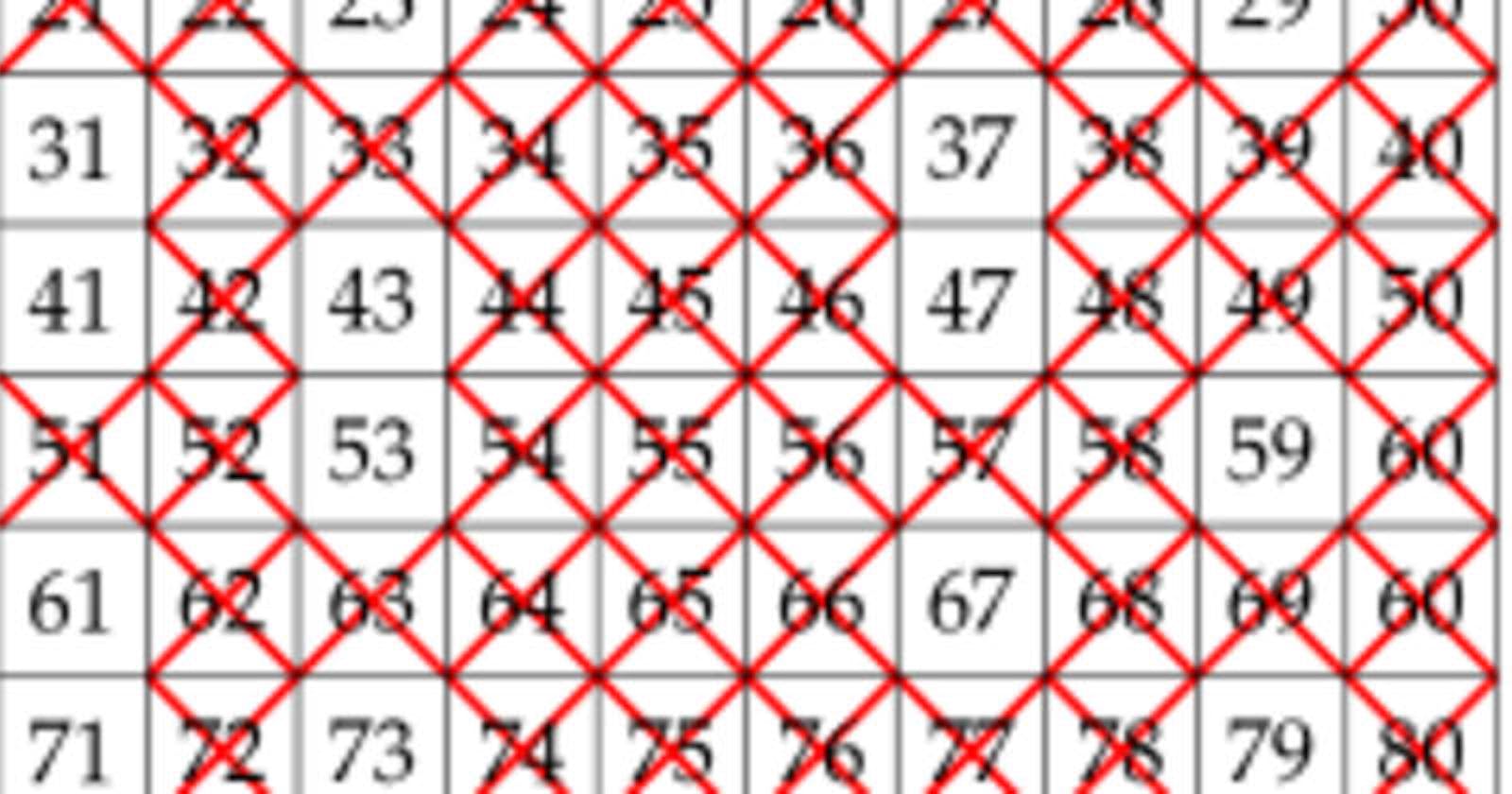
It does so by iteratively marking as composite the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime.

Instead of checking every number as prime(brute force approach), we would work on the groups. First, we will create a vector of boolean values where all values are true. The rest of the work is going to be on this vector only.

The length of the vector is equal to the limit up to which we find all prime numbers, say N. Now, in that vector, assign all the even index starting from 3 as false as all even numbers except 2 are non primes.

Now, for all odd numbers, mark their multiples as false as well as they are non prime as well.

Now mark 0th and 1st index as false as well.

All other indexes set to true are the prime numbers upto N.

#include <bits/stdc++.h>
using namespace std;

void sieveOfEratosthenes(int n)
{
    // Create a boolean array of length n+1 for all numbers from 0 to n
    bool isPrime[n + 1];
    // Set all the elements to true in the isPrime array
    memset(isPrime, true, sizeof(isPrime));

    for (int p = 2; p * p <= n; p++)
    {
        // If isPrime[p] is true, then it is a prime
        if (isPrime[p] == true)
        {
            // Update all multiples
            // of p greater than or
            // equal to the square of it
            // numbers which are multiple
            // of p and are less than p^2
            // are already been marked.
            for (int i = p * p; i <= n; i += p)
                isPrime[i] = false;
        }
    }
    for (int p = 2; p <= n; p++)
        if (isPrime[p])
            cout << p << " ";
}

// Driver Code
int main()
{
    int n = 30;
    cout << "Prime numbers smaller "
        << " than or equal to " << n << endl;
    sieveOfEratosthenes(n);
    return 0;
}

Time complexity of classic Sieve of Eratosthenes algoeithm is O(N log (log N)). Many variations of this algorithm can also be found with even better time complexities.

Read the original article here

Read more such articles here